

 |
Gesetze, Verordnungen, Erlasse und Kommentare
|
 |
Lehrhilfe
Karl Aschersleben
Zur
Statistik der Schulnotengebung
Quelle: Die Deutsche Schule; Hermann Schroedel
Verlag, Hannover, Heft 11/1970 S.761)
Seit einigen Jahren sind Psychologie und Pädagogik in verstärktem Maße bemüht, die Schulnoten objektiver und reliabler zu machen. Unter dem Schlagwort „Objektivierte Leistungsmessung in der Schule” (Gaude und Teschner) werden die Schülerleistungen quantifiziert und Methoden aus der mathematischen Statistik auf die Schulpraxis übertragen. Für den Lehrer ergibt sich die Konsequenz, Grundkenntnisse aus diesem Fachbereich zu erwerben, um die Methoden der Statistik sachkritisch und gegenstandsgemäß anwenden zu können. Mit dieser neuen Wendung entfallen viele kritische Diskussionspunkte gegenüber der bisherigen Benotungspraxis, wie sie u.a. von Stroh (1962), Flitner (1966) oder Ingenkamp (1970) erhoben werden. Der Verfasser versucht, mit dem folgenden Beitrag eine Hilfe zur Überwindung mancher Probleme der Schulnotenpraxis zu geben. Er hält sich dabei eng an Kriterien, die der psychologischen Testtheorie und der angewandten Statistik entnommen sind, und versucht, die bisherigen Ansätze von Stroh (1962), Roeske (1968), Kaiser (1970) und Seelig (1970) zu erweitern.
1. Traditionelle Benotungsverfahren
In der bisherigen Schulpraxis lassen sich zwei Methoden unterscheiden, mit denen der Lehrer Klassenarbeiten benotet.
1. Die apriori-Entscheidung:
Hierbei legt der Lehrer im vornherein fest, welche Fehler- oder Punktzahl in einer Arbeit notwendig ist, um eine bestimmte Zensur zu erhalten. Ein Beispiel: In einem Diktat gibt der Lehrer für 0 Fehler ein ,Sehr Gut’, für 1 bis 2 Fehler ein ,Gut’, für 3 bis 4 Fehler ein ,Befriedigend’, für 5 bis 7 Fehler ein ,Ausreichend’, für 8 bis 10 Fehler ein ,Mangelhaft’ und für mehr als 10 Fehler ein ,Ungenügend’. Eine solche apriori-Entscheidung läßt sich aus der derzeitigen Definition der Notenstufen nach dem Beschluß der Kultusministerkonferenz vom 3.10.1968 ableiten: die Notengebung habe sich danach zu orientieren, inwieweit die Leistung des Schülers bestimmten Anforderungen des Unterrichts entspricht. Da jedoch in den einzelnen Unterrichtsfächern Lernziele im Sinne der Curriculumforschung nicht genügend formuliert und operationalisiert worden sind, bleibt die apriori-Entscheidung von der Subjektivität des Lehrers abhängig. Darüber hinaus werden leichte Arbeiten zu gut und schwere Arbeiten zu schlecht beurteilt, weil ein objektiver Vergleichsmaßstab fehlt. Als statistische Konsequenz ergibt sich, daß gute Arbeiten nicht genügend zwischen den besseren Schülern und schlechter ausgefallene Arbeiten nicht genügend zwischen den schwächeren Schülern diskriminieren. Im ersten Fall ist die Notenverteilung wie auch die Fehler- oder Punktverteilung nämlich linksschief, im zweiten Fall rechtsschief.
2. Mittelwertberechnung:
Lehrer, die sich in ihren Entscheidungen nicht von subjektiven
Vorentscheidungen leiten lassen wollen und die leichte resp. schwere
Klassenarbeiten unterscheiden möchten, benutzen als Orientierungsmaß
für die Benotung das arithmetische Mittel
![]() , indem sie die Gesamtzahl der Fehler oder Punkte einer Arbeit
∑X durch die Schülerzahl N dividieren. Ein Beispiel: In einer Klasse
mit N = 40 Schülern ergibt sich bei einer Rechenarbeit folgende
Punkteverteilung (f = Häufigkeit je Punktzahl, X = jeweilige Punktzahl):
, indem sie die Gesamtzahl der Fehler oder Punkte einer Arbeit
∑X durch die Schülerzahl N dividieren. Ein Beispiel: In einer Klasse
mit N = 40 Schülern ergibt sich bei einer Rechenarbeit folgende
Punkteverteilung (f = Häufigkeit je Punktzahl, X = jeweilige Punktzahl):
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 14 | 16 |
| f | 1 | 1 | - | 2 | 2 | 1 | 4 | 5 | 6 | 7 | 6 | 3 | 2 |
Da ∑X = 467 und N = 40 sind, erhält man
|
= | ∑X | = | 467 | = 11,7 | |
| N | 40 |
Für die Benotung ergeben sich mindestens drei Möglichkeiten:
| A | B | C | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Für welchen der drei Vorschläge sich der Lehrer entscheidet oder ob er eine vierte oder fünfte Möglichkeit wählt, ist eine Ermessensfrage. Das heißt, auch der Bezug auf das arithmetische Mittel bleibt subjektiv, es wird allenfalls eine klassenimmanente Benotung erreicht, wobei die Durchschnitts-Punktzahl von ca. 12 Punkten als Grundlage für eine befriedigende oder ausreichende Leistungsbewertung genommen wird. In Beispiel A und C wird etwa die Durchschnittsleistung zur unteren Grenze des Befriedigend und in Beispiel B zur oberen Grenze des Ausreichend. Die subjektive apriori-Entscheidung wird mit der Methode des arihtmetischen Mittels zwar vermieden, aber es entstehen neue Schwierigkeiten, die sich als Fragen wie folgt formulieren lassen:
| a) | Wie kann eine klassenimmanente Beurteilung vermieden werden, also eine Beurteilung, die mit dem arithmetischen Mittel der einzelnen Klasse arbeitet und deshalb nur Vergleiche der Schüler innerhalb dieser einen Klasse erlaubt? |
| b) | Welchem Notenwert sollte das arithmetische Mittel prinzipiell zugeordnet werden, um die Subjektivität des Lehrerurteils zu verringern? Wie groß sollte der prozentuale Anteil der Benotungen in jeder Zensurenstufe sein? |
Die beiden Fragen lassen sich a) durch Einsatz von Standardarbeiten oder standardisierten Schulleistungstests und b) mit differenzierteren statistischen Methoden beantworten (siehe mit teilweise anderen Ansätzen auch Wendeler, 1969).
a) Die Vermeidung klassenimmanenter Beurteilungen
Da in der klassenimmanenten Beurteilung der Schüler nur mit seinen Mitschülern aus derselben Klasse verglichen wird, sind Vergleiche mit anderen Klassen oder gar mit der Grundgesamtheit aller Schüler in der BRD nicht möglich. Daß dies trotzdem allgemein geschieht, ist pädagogisch nicht zu verantworten. Eine Hilfe zur Überwindung dieses Mangels sind die sog. Standardarbeiten, wie sie vom Soltauer Arbeitskreis für Leistungsmessung in der Schule unter Glatz oder von Lotter entwickelt wurden. Allerdings arbeiten beide Autoren nur mit dem arithmetischen Mittel, Lotter bezieht sich auch ohne weitere statistische Absicherung auf die Normalverteilung, Streuungsmaße werden jedoch von beiden nicht berechnet und die Rohwerte (Fehler oder Punktzahlen) nicht transformiert, auch fehlen Angaben über Eichstichproben. Eine unter testtheoretischen Gesichtspunkten bessere Prüfung der Schülerleistungen ermöglichen z.B. die standardisierten Schulleistungstests des Beltz-Verlags (Weinheim) oder die Rechtschreibtests von Jäger. Mit Hilfe der eben genannten Verfahren kann der Lehrer nicht nur die derzeitige Leistungsgüte seiner Klasse objektiv und reliabel überprüfen, sondern darüber hinaus kann er nun auch die Benotung der Klassenarbeiten auf die Grundgesamtheit aller Schüler in der BRD beziehen. Leistungsschwache Klassen werden entsprechend strenger, leistungsstarke Klassen werden entsprechend milder bei den üblichen selbstkonstruierten Diktaten, Rechenarbeiten oder Sachkundearbeiten beurteilt. Das soll am Beispiel der Rechenarbeit aus dem vorigen Abschnitt erläutert werden. Aus Vergleichsarbeiten des Soltauer Arbeitskreises und aus standardisierten Schulleistungstests weiß der Lehrer, daß die Durchschnittsleistungen seiner Klasse im Rechnen einem Ausreichend entsprechen, d.h. seine Klasse gehört zu den leistungsschwächeren Schulklassen. Er wird also etwas strenger benoten und sich im obigen Beispiel eher für das Beispiel B als für die Möglichkeit A oder C entscheiden.
b) Objektivierung des Lehrerurteils durch Flächen-Transformation
Wie Veröffentlichungen von Ingenkamp, Seelig u.a. zeigen, gewinnt die Transformation von Daten für die Benotung von Schülerleistungen immer mehr an Bedeutung. Was ist eine Transformation? Eine Transformation verändert den numerischen Wert eines Rohwertes (z.B. Fehler- oder Punktzahl) eines Probanden, indem sie ihn nach bestimmten statistischen Kriterien und Methoden einer Skala zuordnet (z.B. der Notenskala), ohne jedoch seine relative Position innerhalb der Gruppe oder Grundgesamtheit zu verändern. Die Zuordnung etwa einer Fehlerzahl des Schülers A zu der Notenskala ist ein statistischer Vorgang, der dem Lehrer im Schulalltag Routine ist. Neu ist, daß die angewandte Statistik ihm Kriterien und Methoden in die Hand gibt, die die Transformation - hier die Schulnotentransformation - zu einem wichtigen Verfahren bei der Objektivierung des Lehrerurteils machen. Diese statistischen Kriterien und Verfahren erst machen die Zuordnung zur Transformation oder Normierung. Sie lassen sich nach der bisherigen Praxis aus einem Hauptkriterium ableiten: die Verteilung der Noten soll einer theoretischen Verteilung, der sog. Normalverteilung, genügen (siehe auch Guilford, 1950). Dazu wird die derzeit gültige sechsstufige Zensurenskala so aufgeteilt, daß jeder Notenstufe ein bestimmter Prozentsatz der Schülerleistungen zugeordnet werden kann. Man erhält damit die sog. Stasix-Normen (Standard-Six in Anlehnung an eine andere Normart, die Stanine oder Standard-Nine-Normen). Die Schülerleistungen verteilen sich wie folgt auf die sechs Notenstufen:
| Notenstufe | I | II | III | IV | V | VI |
| Prozentsatz | 9% | 16% | 25% | 25% | 16% | 9% |
Dabei geht man von einem Mittelwert
![]() = 3,5 und einer Standardabweichung s = 0,75 aus. Für unser
Beispiel einer Rechenarbeit - ohne die notwendige strengere Beurteilung zu
berücksichtigen - folgt die Verteilung:
= 3,5 und einer Standardabweichung s = 0,75 aus. Für unser
Beispiel einer Rechenarbeit - ohne die notwendige strengere Beurteilung zu
berücksichtigen - folgt die Verteilung:
| Notenstufe | I | II | III | IV | V | VI |
| Zahl der Schüler | 5 | 6 | 13 | 9 | 5 | 2 |
| Prozentsatz | 13% | 15% | 33% | 23% | 13% | 5% |
| Punktzahl | 15-16 | 14 | 12-13 | 10-11 | 7-9 | 4-5 |
Bei kleiner Probandengruppe und geringer Streuung der Rohwerte, hier der Punktwerte der Schüler, ist zu berücksichtigen, daß die ermittelten Prozentsätze nur angenähert den erwarteten entsprechen können.
Diese neuerdings in der schulpädagogischen Literatur propagierten
Stasix-Normen haben einen schwerwiegenden
Nachteil: sie genügen nur bei kleinen Probandengruppen noch der
Normalverteilungshypothese. Bereits bei Gruppen von 70 und mehr Probanden wird
die Verteilung wegen der geraden Zahl an Notenstufen zu breitgipflig. Bei
Breitgipfligkeit einer Verteilung spricht man von einem übernormalen
Exzeß. Ob der Exzeß einer Verteilung signifikant oder
überzufällig groß ist, läßt sich (Lienert, 1967,
S.172 und Weber, 1967, S.105ff) mit dem t-Test überprüfen. Danach
folgt, das Stasix-Normen allenfalls bei Transformationen in einzelnen
Schulklassen statistisch gerechtfertigt sind. Die Breitgipfligkeit einer
Normalverteilung läßt sich nun vermeiden, wenn man eine ungerade
Zahl von Klassen, hier Notenstufen, wählt, wie dies bei der
Schulnotenstufen-Transformation (SN) mit nur fünf Notenstufen der Fall ist
(siehe dazu Lienert, 1962 und 1967). Entsprechend der
Normalverteilungshypothese werden die Schülerleistungen wie folgt
prozentual den fünf Notenstufen zugeordnet, wobei Mittelwert
![]() = 3 und s = 1 ist:
= 3 und s = 1 ist:
| Notenstufe | I | II | III | IV | V |
| Prozentsatz | 7% | 24% | 38% | 24% | 7% |
Kelley gibt folgende Prozentsätze für eine fünfstufige Skala an (nach Wendeler, S.69):
| Notenstufe | I | II | III | IV | V |
| Prozentsatz | 10% | 23,3% | 33,3% | 23,3% | 10% |
Diese prozentuale Verteilung entspricht nicht den Voraussetzungen, die
eine Transformation erfüllen muß, wenn
![]() = 3 und s = 1 sind. Bei der Verteilung nach Kelley wird s
größer als 1 und überschreitet damit die Grenzen der
fünfstufigen Notenskala.
= 3 und s = 1 sind. Bei der Verteilung nach Kelley wird s
größer als 1 und überschreitet damit die Grenzen der
fünfstufigen Notenskala.
Welche Leistungen sind in beiden SN-Transformationen nun als ungenügend zu bezeichnen, wie dies bekanntlich von der in der BRD gebräuchlichen sechsstufigen Skala erwartet wird? Hier bietet sich ein Weg als Lösung an, der sich aus den Glatzschen Untersuchungen ableitet: Leistungen, die sehr weit unter dem Klassendurchschnitt liegen, werden als ungenügend bezeichnet und von der weiteren statistischen Bearbeitung ausgeschlossen. Diese Lösung ist auch aus statistischen Gründen zu empfehlen. Denn bei der Transformation von Fehlerzahlen oder Punktwerten bleibt, da es sich um eine Flächentransformation handelt, unberücksichtigt, ob einige Daten sehr weit oder nicht weit vom Mittel abweichen. Dies gilt vor allem, wenn einige Klassen unbesetzt bleiben. Im Beispiel der obrigen Rechenarbeit ist es zum Beispiel die Punktzahl 6, die kein Schüler erreicht hat. Nun werden bei der Flächentransformation die niedrigeren Werte so behandelt, als seien sie um einen Punkt besser. In der Flächentransformation darf keine ,Lücke’ zwischen den Klassen sein, weil man die Verteilung als eine kontinuierliche Verteilung behandelt.
Welche Punktwerte können nun aber in unserem Beispiel als starke
Abweichung vom Klassendurchschnitt bezeichnet werden? Zuerst suchen wir die
beiden Klassenarbeiten heraus, die weit unter dem Klassenmittel von
![]() = 11,7 Punkten liegen, das sind die beiden Arbeiten mit je vier und
fünf Fehlern. Wie kann objektiv entschieden werden, ob diese Arbeiten
„aus dem Rahmen” fallen, um mit einem ,Ungenügend’
beurteilt zu werden? Nach Glatz kommen für ein Ungenügend auch
Arbeiten mit 3, 4, 5 oder manchmal mehr Punkten in Frage, ohne daß jedoch
objektive Kriterien gegeben werden.
= 11,7 Punkten liegen, das sind die beiden Arbeiten mit je vier und
fünf Fehlern. Wie kann objektiv entschieden werden, ob diese Arbeiten
„aus dem Rahmen” fallen, um mit einem ,Ungenügend’
beurteilt zu werden? Nach Glatz kommen für ein Ungenügend auch
Arbeiten mit 3, 4, 5 oder manchmal mehr Punkten in Frage, ohne daß jedoch
objektive Kriterien gegeben werden.
Obwohl wir also nicht wissen, nach welchen objektiven Kriterien wir entscheiden können, welche Arbeiten mit einem Ungenügend bezeichnet werden können, sollen sie beide in unserem Beispiel vor der weiteren Berechnung ausgeschieden werden. Dann erhält man folgende Verteilung mit dem Grundwert N - 2 = 38:
| Notenstufe | I | II | III | IV | V | VI |
| Zahl der Schüler | 2 | 9 | 13 | 10 | 4 | 2 |
| Prozentsatz | 5% | 24% | 34% | 26% | 11% | - |
| Punktzahl | 16 | 14-15 | 12-13 | 9-11 | 7-8 | 4-5 |
Die so durchgeführten Transformationen sind zwar sehr viel objektiver als die traditionellen Verfahren, lassen jedoch noch Fragen offen: Mit welcher objektiven Methode kann man bestimmen, welche Schulleistungen als ungenügend zu bewerten sind?
Wie lassen sich unterschiedliche Abweichungen der Leistungen vom Durchschnitt angemessen beurteilen?
Beide Fragen können mit Hilfe von Methoden beantwortet werden, wie sie in der linearen Transformation - auch einfache Skalierung - verwandt werden.
2. Objektive Zensuren durch lineare Transformation
Zuerst noch einige Anmerkungen zur Funktion von Normen oder Skalenwerten. Rohwerte, d.h. Fehler- oder Punktwerte, haben zwei Nachteile:
Skalenwerte oder Normen beheben diese Mängel, weil sie erstens sinnvoll und zweitens vergleichbar sind. So wird eine ,Zwei’ in der BRD als eine ,gute’ Leistung, eine ,Fünf’ als eine ,mangelhafte’ Leistung usf. interpretiert, irgendeine Fehlerzahl in einem Diktat sagt dem Leser noch nichts. Erst die Transformation dieses Rohwertes in einen Normen- oder Skalenwert macht ihn sinnvoll und vergleichbar (Beispiel aus der Psychologie ist der IQ). Normwerte aus der Flächentransformation sollen nun hinsichtlich ihres Mittelwertes, ihrer Streuung und ihrer Verteilungsform vergleichbar sein, für lineare Transformation gilt nur die der Vergleichbarkeit ihres Mittelwertes und ihrer Streuung (siehe Guilford, 1950, S.288ff). Schulnoten können als Normwerte interpretiert werden und unterliegen dann denselben Voraussetzungen wie etwa IQ-, T- oder Z-Normen. Auf eine Vergleichbarkeit der Verteilungsform kann nach Ansicht des Verfassers verzichtet werden, weil es dafür keine zwingende Begründung gibt.
Die Methode der linearen Transformation soll an einem Beispiel erläutert werden. Als Beispiel wählen wir ein Diktat in einer Klasse mit N = 42 Schülern (f = Häufigkeit pro Fehlerzahl):
| Fehlerzahl | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ... | 17 |
| f | 2 | 4 | 3 | 5 | 4 | 2 | 6 | 4 | 5 | 3 | - | 2 | - | 1 | 1 |
Im Unterschied zur Methode der Flächentransformation benötigen wir keine Prozentsätze als Orientierungshäufigkeiten. Auch will die lineare Transformation nicht der Hypothese der Normalverteilung genügen, das heißt, wir verändern in unserem Beispiel nicht die leicht zweigipflige Verteilung unserer Fehler, vielmehr wird sie für die Transformation übernommen, und es werden die Werte nur hinsichtlich Mittelwert und Streuung verändert. Auch werden die Extremwerte mit 11, 13 und 17 Fehlern nicht wie in der Flächentransformation an die anderen Werte herangeschoben und die Verteilungsstreuung nicht unnötig verringert. Darüber hinaus erlaubt die lineare Transformation eine objektive Beurteilung auch ungenügender Leistungen und eine ebenso objektive Zuordnung der Klasse zur Grundgesamtheit oder Population, vorausgesetzt, ihre Leistungsstärke ist durch standardisierte Tests u.ä. bekannt.
Zuerst wird das arithmetische Mittel X nach der bekannten Formel berechnet:
|
= | ∑X | , | |
| N |
anschließend die Standardabweichung s nach der Formel
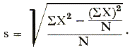
Die Berechnung der Standardabweichung s oder einer anderen Streuung ist für eine statistische Auswertung ebenso wichtig wie die Mittelwertsberechnung, wenn auch bisher weniger in der Schulpraxis bekannt und etwas weniger einfach zu berechnen als die Mittelwerte. Für unser Beispiel erhält man nach Einsetzen in die Formel die Werte:
|
= | ∑X | = | 234 | = | 5,6 | |
| N | 42 |
und für s die Werte
= |
1850 − 2342 : 42 |
= |
13,71 |
|
| 42 | ||||
| S | = | 3,7 |
Für jeden Einzelwert X läßt sich nun der Normwert z berechnen, der uns dann zum SN-Normwert führt. Die Formel lautet:
| Z | = | X –
|
= | X – 5,6 |
| s | 3,7 |
Für jeden Rohwert ergibt sich ein z-Wert, der danach in einen SN-Wert verwandelt werden kann, indem man ihn in die Formel einsetzt:
SN = 3,5 - z.
Dabei ist 3,5 die vorgegebene Mitte der sechsstufigen Notenskala. Weiß der Lehrer, daß seine Klasse um 0,5 Normpunkte unter dem Durchschnitt der Grundgesamtheit liegt, so braucht er die Schulnoten-Skala nur um 0,5 Punkte zu verschieben, um zu einer vergleichbaren Leistungsbeurteilung zu kommen (SNcorr). Die folgende Tabelle veranschaulicht den gemeinten Rechengang:
| Fehler | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ...... | 17 |
| f | 2 | 4 | 3 | 5 | 4 | 2 | 6 | 4 | 5 | 3 | - | 2 | - | 1 | ...... | 1 |
| z | -1,51 | -1,24 | -0,97 | -0,70 | -0,43 | -0,16 | 0,11 | 0,38 | 0,65 | 0,92 | - | 1,46 | - | 2,00 | ...... | 3,54 |
| SN | 1,49 | 1,76 | 2,30 | 2,03 | 2,57 | 2,84 | 2,89 | 3,38 | 3,65 | 3,92 | - | 4,46 | - | 5,00 | ...... | 5,54 |
| SNcorr | 1,99 | 2,26 | 2,53 | 2,80 | 3,07 | 3,34 | 3,39 | 3,88 | 4,15 | 4,42 | - | 4,96 | - | 5,50 | ...... | 6,04 |
| Zensur | II | II | III | III | III | III | III | IV | IV | IV | - | V | - | VI | ...... | VI |
Dieses Beispiel belegt, daß die lineare Transformation dem Lehrer Kriterien in die Hand gibt, mit denen er die Leistungen seiner Klasse objektiv und unter Bezug auf die Grundgesamtheit, also vergleichbar, bewerten kann. Der Rechenweg soll abschließend zu einem Schema zusammengefaßt werden, das für die wichtigsten Klassenarbeiten bei einiger Übung Routineauswertungen ermöglicht:
1. Schritt: Stelle eine Fehler- oder Punkteliste aus den Einzelwerten X zusammen!
2. Schritt: Berechne das arithmetische Mittel
![]() , indem du die Gesamtzahl der Fehler oder Punkte ∑X ermittelst
und diese durch die Zahl der beteiligten Schüler N dividierst:
, indem du die Gesamtzahl der Fehler oder Punkte ∑X ermittelst
und diese durch die Zahl der beteiligten Schüler N dividierst:
X = ∑X , N
3. Schritt: Berechne die Standardabweichung s, indem du von der Summe der quadrierten Einzelwerte ∑X2 den Quotienten aus dem Quadrat der summierten Einzelwerte (∑X)2 und der Schülerzahl N abziehst, das Ergebnis durch die Schülerzahl N dividierst und die Wurzel ziehst:
4. Schritt: Berechne für jeden Punkt-
oder Fehlerwert X den Skalenwert z, indem du
![]() und s in die folgenden Formel einsetzt:
und s in die folgenden Formel einsetzt:
Z = X – s
5. Schritt: Die unkorrigierten SN-Skalenwerte ergeben sich, indem du die z-Werte in die folgende Formel einsetzt:
SN = 3,5 - z
6. Schritt: Falls notwendig, wird bei leistungsstarken Klassen ein konstanter Skalenwert subtrahiert, bei leistungsschwachen Klassen addiert.
7. Schritt: Die auf ganze Zahlen gerundeten SN-Skalenwerte ergeben die Zensur für jeden Fehler- oder Punktwert.
Literatur:
________________
Abdruck mit freundlicher
Genehmigung des Autors
Dr. rer. nat. Karl Aschersleben
(Lehrer,
Hochschuldozent, Lehrbeauftragter Uni Hannover, a.D.),
28.Juli 2010
| Schule und Recht in Niedersachsen (www.schure.de) |